 Super Sudoku Newsletter
Super Sudoku Newsletter
Our first newsletter
This is the first newsletter for Super Sudoku! We will hope to send out one email newsletter every couple of months with lots of interesting Sudoku news. Thank you for all the comments we have had from you about the site. We are considering many of your suggestions and developing new exciting Sudoku features in response.
Say it!
 Since the beginning of our website, we have had a number of emails asking us how to say the word: "Sudoku". Also, we have heard many incorrect pronunciations on TV, over the phone and on Skype. To explain the pronunciation of Sudoku, divide the word into its three syllables:
Since the beginning of our website, we have had a number of emails asking us how to say the word: "Sudoku". Also, we have heard many incorrect pronunciations on TV, over the phone and on Skype. To explain the pronunciation of Sudoku, divide the word into its three syllables:
| su - | like the name "Sue". Sometimes people say "so" here as they think the name is "sodoku", or more commonly, "soduku". |
| do - | as in the UK or Australian English pronunciation of "dock" or the general English pronunciation of "dot" with the "o" not as the word "owe" or "go". |
| ku - | like the word "coup" (with the silent p) or as in the word "cooler". |
Just to make clear, it is not written or pronounced as: su-du-ku, su-du-ko or su-do-ko. I hope this clears up an ambiguity for some of our members.
 Sudoku by email
Sudoku by email
The main features introduced over the last couple of months include a comprehensive email facility and an easy-to-use print function. You can now generate a Sudoku to email to yourself or a friend. When you email a Sudoku to yourself, you may include the solution as a separate attachment. If you want to email a Sudoku or Super Sudoku to a friend, you can accompany the puzzle with your own message. The email facility is available for all Sudoku solvers and generator areas, with full members having fewer restrictions in place. So, have a go and send your Sudoku puzzles to a friend!
Unique and interesting Sudoku
All Sudoku at Sudoku Solver are totally unique, generated just for you and no one else. Every time you press the "generate" button you will get your own special Sudoku to print or share. Behind the scenes is a highly sophisticated Sudoku and Super Sudoku generator performing millions of calculations per second to deliver a puzzle can cannot be matched in terms of solving quality. We ensure that each Sudoku created correctly fits into the difficulty level. We have also moved our Sudoku generator to a super fast Xeon server. You are able create live unique Sudokus in next to no time!
New difficulty levels
Are Sudoku getting a little too easy for you? Since your last visit we have introduced some new Sudoku and Super Sudoku difficulty levels. These range from very easy (slightly easier than the previous "easy" Sudoku) to very hard, bringing you to a new extreme level of Sudoku. Get a full account and try out our very hard Sudoku and Super Sudoku now. This will keep you busy for many hours unlike any other Sudoku puzzle you have tried before.
Super Sudoku solvers
As some publications prefer to keep 4×4 Super Sudoku strictly within the alphabet, we made a subtle change to the Super Sudoku solver — it now accepts letters from A to P as well as numbers 0 – 9 and letters A – F. If a large Sudoku implies a 3×4 grid for you, then don't worry we are developing a new 3×4 Sudoku solver and generator.

 Win a portable DVD player!
Win a portable DVD player!
As you haven't visited supersudoku.com recently, you won't have seen our new Super Sudoku competition. For a chance to get your hands on a Goodmans 7" portable widescreen DVD player, go to our competition page now. It is open to everyone to take part, so take the Super Sudoku challenge and win our cool prize.
Get more Sudoku!
If you want to get more Sudoku out of supersudoku.com, then why not upgrade? It is just a one only payment of £5.00 (€7.60, $9.00) through PayPal. Its very quick and easy to get some of the following features:

- Unrestricted access to all solvers and generators
- Generate up to 15 unique Sudoku daily
- Solve up to 45 Sudoku and Godoku daily
- Generate up to 6 unique Super Sudoku daily
- Solve up to 15 Super Sudoku daily
- Challenge your mind with very hard Sudoku
- Generate medium, hard and very hard Super Sudoku
- Print generated or solved Sudoku, Super Sudoku or Godoku
- Email more generated or solved Sudoku, Super Sudoku or Godoku
- Email more generated Sudoku or Super Sudoku with solutions attached
- View and print solutions to all generated Sudoku or Super Sudoku
So, use this link to upgrade your account straight away!
How many different Sudoku solutions?
Sometimes people ask us: "how many different Sudoku puzzles are there?". To answer this we need to understand that each Sudoku puzzle gives just one unique solution grid. We can say that two Sudoku puzzles are the same if they resulted in the same solution. So, a similar question is: "how many different complete Sudoku solutions are possible?".
First of all, let's first look at a much simpler grid, namely the 2×2 Sudoku with the numbers 1 to 4. The three rules for solving Sudoku still apply: The row rule (place the numbers 1 - 4 in each row), the column rule (place the numbers 1 to 4 in each column) and the subsquare rule (place the numbers 1 - 4 in each subsquare).
On the first row, count how many different ways can we place the numbers 1, 2, 3 and 4 in the row. In the first square, we have four numbers to choose from. In the second square, we have only three numbers to choose from, as we have already placed the previous square. We have two choices for the third square and only one choice for the fourth square as there is only have one number remaining. To find the total number of possible ways, we need to multiply all these numbers together to calculate the total number of permutations (possible ways to order the numbers). So, we have 4×3×2×1 = 24 ways of placing the numbers in the first row. Suppose that we put the numbers in the order 1 2 3 4 so that the Sudoku looks like:

Now, for the second row, we must place the numbers 1 to 4 in some order. There are only two choices for the first square on the second row. There are not four choices because we not only cannot put in a 1 here (as we will have two 1's in the same column), but also we cannot put in a 2 (as we will break the subsquare rule). There is only one choice for the second square because we must keep to the rule of having 1 to 4 in each subsquare. There are two choices for the third square as we have two numbers left to place, and one choice for the fourth square. So using the mathematics of permutations again, there are 2×1×2×1 = 4 different ways to complete the second row of the table. The Sudoku will now look as follows:

For the third row, we must place each of the numbers 1 to 4. We will not have to worry about the subsquare rule in this row, as we are starting the second row of subsquares. Using the same logic as before, we have two choices for the first, second and third squares and one choice for the fourth. However, what happens if we place the first two squares as 2 and 3, then place a 4 in the third square as it cannot go in the fourth square?
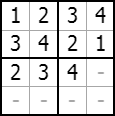
We cannot place the 1 in the last square!
This is why finding the total number of solution squares is difficult. We can calculate the approximate number of solution grids using the method we were using, but in reality there will be less possible grids. For the 2×2 Sudoku grid, there will be 2×2×1×1=4 different ways to order the third row. There is only one way to complete the last row, as we are simply completing the columns using the column rule. So, our maximum number of Sudoku grids (called the upper bound) is: 24×4×4×1 = 384.
If we want to know the exact number of different solution grids that are possible, we will have to write them all out by hand. This isn't actually too difficult. We can just write out all of the ways to complete the grid once we have reached the point:

Whichever numbers are in these first four places, the number of ways to complete the entire Sudoku will be the same. The solution grids will be almost the same, but with the numbers switched. For example, all of the 1's could be replaced by 2's, and all of the 2's will be replaced by 1's (in fact, one could say that if this is the case, then the solution grids are essentially the same). This switch would not affect whether we came to an error later on or not.
Writing out all of the possibilities (which I won't do here), there are only 12 different ways of completing the grid, once the first row has been fixed. Recalculating the total number, we have 24×12 = 288 different solution squares. This is assuming that we do not count rotations and other simple transformations of grids to still be the same grid. We are counting:
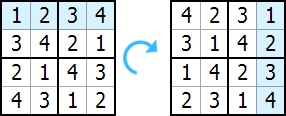
to be different solutions even though the second grid is simply the first grid rotated by 90° clockwise.
Returning to the original question, how many 3×3 Sudoku solution grids are there? Using similar methods to the 2×2 Sudoku example above and using quick estimates (only making sure that we do not appear to break the three rules of Sudoku), we get:
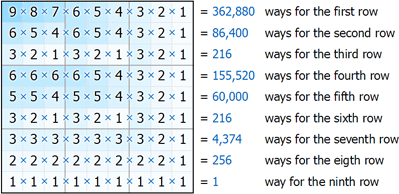
which gives us:
362880×86400×216×155520×60000×216×4374×256×1
= 15,284,122,844,890,207,459,737,600,000,000 solutions!
In reality, there will be many less possible grids than this. To obtain an exact number, we would need to try all of the combinations. As it is impossible to do this by hand, a computer program must be used. This has been done (you can read the paper on 'Enumerating possible Sudoku grids') and apparently there are only 6,670,903,752,021,072,936,960 possible valid solutions. The reason that this number is so much smaller than the estimate obtained above is probably because there are many more ways to arrive at an error when there are more numbers to place.
(This article was inspired by discussions on Sudoku Programmers Forum and Sudoku Players Forum)
Next Super Sudoku newsletter
In the next issue we will have information on being in the audience of several upcoming Sudoku TV shows in the UK, also information on several cool new features in development at Super Sudoku and some interesting news from the wider Sudoku community.
![]()
P.S. If you want to change your newsletter preferences, simply log on to your Super Sudoku account and check/uncheck the newsletter box.



